What are Two Dimensional Arrays
In programming, data is often organized in arrays, which are collections of items stored at contiguous memory locations. A one-dimensional array stores a linear sequence of elements, accessible using a single index. However, we need a more powerful two-dimensional array for more complex data structures, like tables or matrices.
A two-dimensional array is a type of array that allows us to store elements in a tabular form, organized in rows and columns. This makes it ideal for representing grid-like structures, matrices, or any data set with a row and column relationship.
For example, in image processing, a two-dimensional array can represent an image where each element in the array corresponds to a pixel. In game development, two-dimensional arrays, such as a chessboard, are often used to describe the game board.
2. Basic Structure of Two-Dimensional Arrays
A two-dimensional array is often considered a table with rows and columns. Each array element is identified by two indices: one representing the row and the other representing the column.
Visual Representation
Consider a 2D array with 3 rows and 4 columns:
Jagged arrays are more memory-efficient in scenarios where some rows don’t need the same number of elements.
In this example, the element in the first row and second column is 6. The general form for accessing any element in a 2D array is arr[row][column].
Declaration of 2D Arrays
Different programming languages have their syntax for declaring 2D arrays. Below are examples of how two-dimensional arrays are declared in various languages:
- C/C++:
int array[3][4]; // Declares a 3×4 integer array
Python: Python does not have built-in support for 2D arrays, but we can achieve this by creating a list of lists:
matrix = [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]]
-
- Java:
int[][] array = new int[3][4]; // Declares a 3×4 integer array
Memory Layout
Most languages store 2D arrays in row-major order, meaning the elements of each row are stored in contiguous memory locations. Some programming languages, like Fortran, use column-major order. Knowing the memory layout can be crucial for optimizing programs that heavily use 2D arrays, especially for performance-sensitive tasks like matrix multiplication.
3. Accessing Elements in a Two-Dimensional Array
Once you understand the row-column structure, accessing individual elements in a two-dimensional array is simple. The array indices start at 0 in most programming languages (e.g., C, C++, Python, Java). To retrieve or modify an element, specify both the row and column indexes.
Example in Python:
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
print(matrix[1][2]) # Output: 6
Here, matrix[1][2] accesses the element at the row index 1 and column index 2, which is 6.
Nested Loops for Traversal
Nested loops are commonly used to iterate over all elements in a 2D array. The outer loop iterates over the rows, and the inner loop iterates over the columns.
Nested loops are commonly used to iterate over all elements in a 2D array. The outer loop iterates over the rows, and the inner loop iterates over the columns.
Example in C++:
for(int i = 0; i < 3; i++) {
for(int j = 0; j < 4; j++) {
cout << array[i][j] << ” “;
}
cout << endl;
}
This loop prints each element of the array array[i][j] in row-major order.
4. Applications of Two-Dimensional Arrays
1. Matrices in Mathematics
In mathematics, matrices are often represented using two-dimensional arrays. Matrix operations like addition, subtraction, and multiplication are essential in various fields, including graphics programming, cryptography, and data science.
Example of Matrix Multiplication:
Consider two matrices A and B, where A is a 2×3 matrix and B is a 3×2 matrix. The product matrix C will be a 2×2 matrix, where each element is the dot product of a row from A and a column from B.
In C++, matrix multiplication can be implemented like this:
int A[2][3] = {{1, 2, 3}, {4, 5, 6}};
int B[3][2] = {{7, 8}, {9, 10}, {11, 12}};
int C[2][2] = {0};
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
for (int k = 0; k < 3; k++) {
C[i][j] += A[i][k] * B[k][j];
}
}
}
2. Image Representation
Images are represented as grids of pixels, which can be thought of as a 2D array of color values. Each pixel is an element in the array, and its value can represent the grayscale intensity or color information (e.g., RGB values).
For example, a 3×3 grayscale image can be stored in a 2D array like this:
image = [[0, 255, 0],
[255, 0, 255],
[0, 255, 0]]
Each value represents the intensity of the corresponding pixel, with 0 being black and 255 being white.
3. Game Development (Grids and Maps)
In many games, a two-dimensional array is used to represent a game board or map. For instance, a chessboard, which is an 8×8 grid, can be represented as:
int[][] chessboard = new int[8][8];
Each element can represent a different piece, like 1 for a pawn, 2 for a knight, and so on.
5. Operations on Two-Dimensional Arrays
1. Traversing a 2D Array
Traversing a two-dimensional array is done using nested loops, as shown earlier. This operation is fundamental for reading or modifying the elements of the array.
2. Searching in a 2D Array
Searching for a specific element in a 2D array typically involves checking each element one by one. This is called linear search, and its time complexity is O(nm) for a variety of size nm.
3. Sorting a 2D Array
Sorting can be done row-wise or column-wise. Sorting row-wise means sorting the elements within each row, and sorting column-wise means arranging the elements in each column.
4. Matrix Transposition
Matrix transposition involves swapping rows with columns. For example, the transposition of the matrix A:

would be:

Here’s an example of how transposing can be implemented in Python:
matrix = [[1, 2, 3], [4, 5, 6]]
transpose = [[matrix[j][i] for j in range(len(matrix))] for i in range(len(matrix[0]))]
6. Jagged Arrays (Array of Arrays)
A jagged array is an array of arrays where each sub-array can have a different length. It’s useful when the data structure needs varying row lengths. In C#, for example:
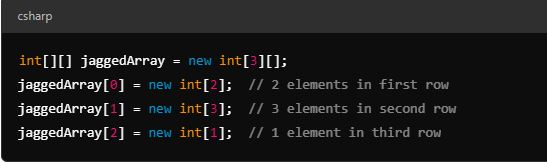
Jagged arrays are more memory-efficient in scenarios where some rows don’t need the same number of elements.
7. Optimization Techniques of Two Dimensinal Arrays:
Sparse Matrices
If the 2D array contains a lot of zero elements, representing it as a sparse matrix can save memory. A sparse matrix only stores non-zero elements and their positions.
For example, the following matrix:

can be represented as:
- Non-zero elements:
[(0, 2, 3), (1, 1, 5)], where each tuple stores the row index, column index, and value.
9. Advantages and Limitations of Two Dimensional Arrays
Advantages:
Two-dimensional arrays are popular due to their simplicity and effectiveness for certain types of problems. Here are some of their key advantages:
- Easy to Understand and Use:
- Two-dimensional arrays offer a clear and intuitive way to store and access data. The tabular structure closely mirrors how we think about data in rows and columns, making it easier for beginners and experienced programmers alike to work with.
- For example, a 2D array can be used to represent a chessboard or a tic-tac-toe game grid. Each piece or move can be mapped directly to an element in the array based on its row and column position.
- Fixed Size and Memory Allocation:
- Since 2D arrays are statically sized in most programming languages, their memory allocation is done at compile time (in languages like C/C++). This provides predictable memory usage, which is essential for systems where memory management is critical.
- Static memory allocation also results in faster access times because the array elements are stored in contiguous memory locations, reducing the overhead of dynamic memory management.
- Efficient Access:
- Accessing elements in a two-dimensional array is very efficient, with a constant time complexity of O(1) for retrieving any element, assuming you know the indices. This is because the array index is directly mapped to a specific memory address.
- In contrast, accessing elements in more complex data structures, such as linked lists or hash tables, may involve traversal or hashing operations, which can take longer.
- Matrix Operations:
- In scientific computing, two-dimensional arrays are fundamental for performing matrix operations like addition, subtraction, and multiplication. Many problems in fields like physics, engineering, and computer graphics can be modeled using matrices, which are naturally implemented using 2D arrays.
Limitations Of Arrays:
While two-dimensional arrays are powerful, they come with certain limitations that can impact performance and flexibility in some applications:
- Fixed Size:
- In most languages, the size of a two-dimensional array must be specified when it is declared. This makes the array static, meaning it cannot grow or shrink during runtime. If the number of rows or columns needed changes, you must reallocate memory or create a new array.
- For example, if you declare an array as
int matrix[100][100];and only end up using 10 rows and 10 columns, you waste memory on the unused space. This is particularly inefficient for large datasets where sparse arrays (with many zeros or empty entries) are common.
- Memory Inefficiency for Sparse Data:
- When working with sparse datasets, where many of the elements in the 2D array are empty or zero, the fixed-size structure of a 2D array leads to wasted memory. For example, in a 1000×1000 matrix representing a network graph where only a few nodes are connected, a large portion of the array will remain unused.
- This can be mitigated by using sparse matrix representations, where only the non-zero elements and their coordinates are stored. However, this involves more complex data structures like linked lists or dictionaries, which take longer to access compared to direct array indexing.
- Lack of Flexibility:
- In situations where the size of the data is unknown or may vary during execution, 2D arrays are not the best choice. Dynamic data structures like lists of lists (in Python) or vectors of vectors (in C++) allow resizing, inserting, and deleting elements more efficiently.
- For instance, if you’re managing a grid where rows or columns might be added or removed dynamically (such as in spreadsheet applications), dynamic structures are better suited than static arrays.
- Inefficient for Complex Data Types:
- Two-dimensional arrays are well-suited for simple data types like integers or floats. However, for storing more complex objects or non-rectangular data, 2D arrays can be cumbersome to work with. In such cases, jagged arrays or dynamic arrays are more appropriate because they allow for flexible row lengths and can handle more complex data structures.
10. Alternatives to Two-Dimensional Arrays
In programming, certain situations call for more flexible or efficient data structures than a two-dimensional array. Here are some common alternatives:
- Jagged Arrays:
- A jagged array is an array of arrays where each “row” can have a different number of columns. This structure provides flexibility when the size of each row varies. It’s commonly used when working with sparse data or when rows contain varying amounts of data.
- Example (C#)
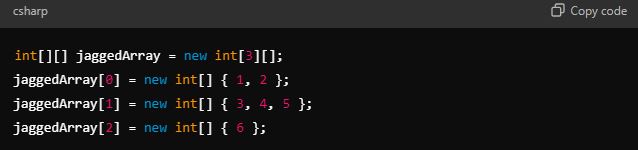
- Jagged Arrays:
- Two-dimensional arrays are well-suited for simple data types like integers or floats. However, for storing more complex objects or non-rectangular data, 2D arrays can be cumbersome to work with. In such cases, jagged arrays or dynamic arrays are more appropriate because they allow for flexible row lengths and can handle more complex data structures.
- Easy to Understand and Use:
2. Dynamic Arrays (Lists in Python, Vectors in C++):
- Unlike fixed-size arrays, dynamic arrays can grow or shrink during runtime. This makes them more suited to situations where the amount of data is unknown or may change over time.
- Python Example:
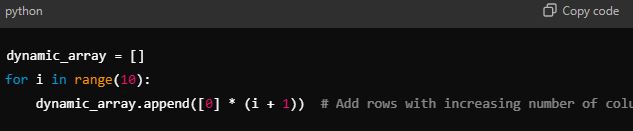
3 . Sparse Matrices:
-
- For scenarios involving sparse data, sparse matrices are more efficient than 2D arrays. A sparse matrix only stores non-zero elements and their positions, making them ideal for scenarios where most of the data is zero or irrelevant.
- Common implementations of sparse matrices include:
- Coordinate list (COO format): Stores a list of tuples, each containing the row, column, and value of non-zero elements.
- Compressed Sparse Row (CSR format): Stores non-zero elements by rows, improving memory efficiency for certain matrix operations like matrix multiplication.
4 . Linked List or Hash Map:
- For non-grid-like data that needs to be accessed and modified dynamically, linked lists or hash maps are often better choices than arrays. They allow more flexible data storage and dynamic resizing without the rigid structure of an array.
11. Optimization Techniques for Two-Dimensional Arrays
Two-dimensional arrays can be optimized in different ways, depending on the context and the specific operations you’re performing. Here are some strategies for optimizing the usage of 2D arrays:
- Memory Efficiency with Sparse Matrices:
- As mentioned earlier, sparse matrices are a powerful way to save memory when dealing with large matrices that contain many zeros. By using a data structure that only stores non-zero values and their coordinates, you can reduce the space complex
- Python Example Using Scipy Library:
from scipy.sparse import csr_matrix
matrix = csr_matrix([[0, 0, 3], [4, 0, 0], [0, 5, 6]])
print(matrix)
2. Optimizing Traversal:
- Traversing a two-dimensional array can be optimized by considering its memory layout (row-major or column-major). Accessing elements in the order they are stored in memory (row-major for most languages like C and Python) minimizes cache misses and improves performance.
- In matrix multiplication scenarios, block-based traversal or loop unrolling can further optimize performance.
3. Avoiding Repeated Calculations:
-
- When performing matrix operations like multiplication or transposition, redundant calculations can slow down your program. Using techniques like memoization (storing previously calculated results) can save time in complex algorithms.
- Example: In dynamic programming algorithms like matrix chain multiplication, storing intermediate results in a table (which can be represented as a 2D array) avoids recalculating the same subproblems repeatedly.
4. Parallel Processing:
-
-
- Leveraging parallelism can greatly improve performance for large-scale matrix operations. Libraries like OpenMP (in C/C++) or multiprocessing (in Python) allow the distribution of array computations across multiple CPU cores.
-
OpenMP Example (C++):
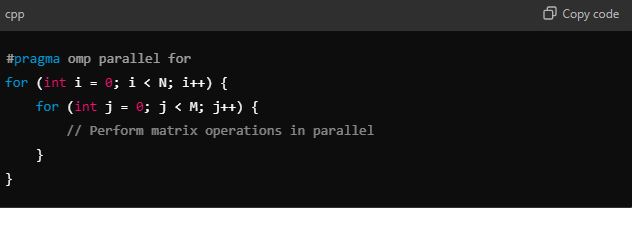
12. Conclusion
In conclusion, two-dimensional arrays are a fundamental data structure in computer science, offering a straightforward and efficient way to store and manipulate data in a grid-like format. They are particularly useful in scenarios involving matrices, tabular data, game boards, image processing, and scientific computing.
The ease of access, intuitive structure, and fixed-size memory allocation make 2D arrays a go-to choice for many applications. However, they come with limitations, especially when it comes to flexibility and memory efficiency for sparse data. As we’ve discussed, alternatives like jagged arrays, dynamic arrays, and sparse matrices provide solutions to some of these limitations.
Optimization techniques like memory-efficient storage for sparse matrices, parallel processing, and efficient traversal are crucial when working with large datasets or performance-sensitive applications. Understanding when and how to apply these techniques is key to making the most out of two-dimensional arrays.
As the world of programming evolves, with the growing demand for handling larger and more complex data structures, mastering the use of two-dimensional arrays and knowing when to use more advanced data structures will help programmers tackle a wide range of problems efficiently and effectively.
